在数字资产的世界里，secp256k1椭圆曲线算法如同每个人的独特指纹，守护着价值万亿美元的加密资产安全。就像指纹锁通过生物特征识别确保物理安全一样，这条数学曲线通过数字签名技术为区块链交易提供不可伪造的身份认证。

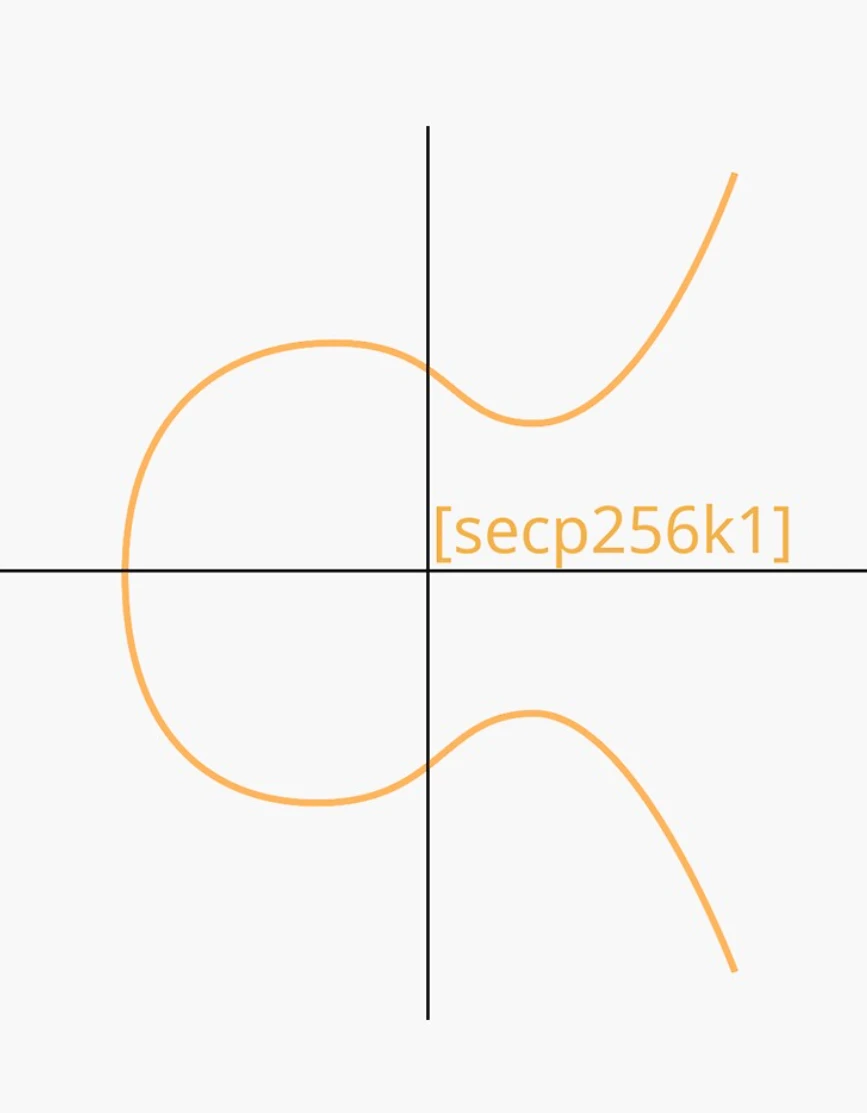
作为比特币、以太坊等主流加密货币的底层密码学基石，secp256k1曲线承载着全球加密经济的信任基础。其名称中的"256"代表256位素数的安全强度，"k1"则标志着它是SECG标准中的第一条Koblitz曲线。这条看似简单的数学曲线y²=x³+7，为何能成为价值万亿数字资产的守护神？其背后隐藏着怎样的密码学奥秘？让我们揭开这段数字传奇的面纱。

椭圆曲线家族的特种兵

在密码学的武器库中，secp256k1犹如一位经过特殊训练的特种兵，其独特的数学构造赋予了它非凡的加密能力。

1. 解密数学公式y²=x³+7背后的密码学意义

这条看似简单的椭圆曲线方程y²=x³+7（mod p）实则暗藏玄机。其中模运算（mod p）将曲线限制在有限域内，使得离散对数问题变得异常困难。这种单向计算特性，正是数字签名不可伪造性的数学基础。

2. 解析"256位素域"如何构建数字保险箱

曲线定义在2²⁵⁶-2³²-2⁹-2⁸-2⁷-2⁶-2⁴-1这个256位素数域上，相当于提供了约1.15×10⁷⁷个可能的点坐标。这个天文数字级的空间，使得暴力破解私钥的尝试在现有计算能力下完全不可行，如同将密钥藏在银河系般庞大的保险箱中。

3. 揭秘Koblitz曲线的特殊计算优势

作为Koblitz曲线家族成员，secp256k1具有可优化的标量乘法运算特性。通过预计算和端乘法优化技术，其签名验证速度比普通曲线快30%以上，这种效率优势在需要高频交易验证的区块链场景中尤为关键。

这条诞生于2000年的椭圆曲线，因其在安全性与效率间的完美平衡，最终成为加密货币世界的标准配置。其数学之美不仅体现在简洁的方程形式上，更在于精妙的设计为数字资产构建了坚不可摧的数学堡垒。

加密货币的基石

2008年，中本聪在比特币白皮书中引入的secp256k1曲线，掀起了一场密码学革命。这条看似简单的数学曲线y²=x³+7，却成为价值万亿美元加密经济的信任基石。

在安全性方面，secp256k1基于椭圆曲线离散对数问题(ECDLP)的数学难题构建防御体系。即便在量子计算时代，256位的密钥空间仍能提供足够的安全屏障。相比传统RSA算法需要3072位密钥才能达到相同安全级别，secp256k1在签名速度上快15倍，验证速度快100倍。与国密标准SM2相比，其特殊的Koblitz曲线特性使签名生成效率提升约30%。

更关键的是网络效应带来的生态壁垒。比特币、以太坊等主流公链的采用，使得secp256k1形成了完整的开发者工具链和标准化体系。这种先发优势如同互联网时代的TCP/IP协议，随着生态规模的扩大而不断强化其主导地位。新项目选择这条曲线，可以直接接入现有钱包、交易所等基础设施，获得即时的互操作性。

从技术特性到生态协同，secp256k1完美诠释了区块链领域"代码即法律"的核心理念。这条数学曲线不仅是算法选择，更是构建去中心化信任的基础协议层。

数字签名的四重奏

1. 私钥生成的随机性艺术

在secp256k1椭圆曲线密码体系中，私钥的诞生堪称密码学领域的随机性杰作。这个256位的随机整数（范围在1到2²⁵⁶-1之间）如同数字世界的基因密码，其生成过程必须满足严格的密码学随机性标准。现代钱包采用硬件熵源配合确定性随机数生成器(DRBG)，确保每个私钥都具备不可预测性。有趣的是，理论上可能的私钥数量比宇宙中原子的总数还要多，这种天文数字级的可能性空间构成了加密货币安全的第一道防线。

2. 公钥推导的单向性魔法

通过椭圆曲线点乘运算Q = d×G（其中d为私钥，G为曲线基点），私钥到公钥的转换展现精妙的单向性特征。这个过程犹如将原料炼成无法逆向解析的加密合金——即便公开曲线参数和公钥Q，想要通过离散对数问题(ECDLP)反推私钥d，其计算复杂度相当于在银河系中寻找特定的一粒沙子。secp256k1曲线精心设计的数学结构，使得这种逆向工程在当前计算能力下需要耗费数十亿年。

3. 交易签名的零知识证明

当用户使用ECDSA算法签署交易时，本质上是在进行一场精妙的零知识证明：签名(r,s)既能证明签名者确实持有对应私钥，又不会泄露任何关于私钥本身的信息。签名过程中引入的临时随机数k（称为nonce）必须绝对保密且不可重复使用，否则可能导致私钥泄露。2020年PlayStation 3系统遭破解的案例，正是由于nonce重用导致的签名体系崩溃，这从反面印证了正确实现签名算法的重要性。

4. 全节点验证的分布式信任机制

区块链网络中的每个全节点都配备完整的secp256k1验证能力，它们通过并行计算验证签名的数学正确性。验证过程需要检查三个核心要素：签名(r,s)是否在有效范围内、公钥是否位于曲线上、以及签名方程是否成立。这种分布式验证机制消除了中心化信任中介，使得全球节点能在无需相互信任的情况下，就交易有效性达成数学共识。据统计，比特币网络每天要处理超过30万笔此类签名验证，secp256k1的高效特性使得普通计算机也能在毫秒级完成验证。

这四重机制环环相扣，共同构建了加密货币不可伪造、不可抵赖的安全特性。从私钥生成到全网验证，secp256k1曲线如同精密的密码学齿轮组，驱动着价值互联网的信任机器持续运转。

超越货币的价值传递

secp256k1椭圆曲线算法正在突破加密货币的边界，在更广阔的数字化领域展现其独特价值。在TLS/SSL协议中，该算法为网站服务器和客户端提供高效的身份认证机制，其256位密钥长度既能确保安全性，又不会显著增加握手延迟。这种特性使其成为现代加密通信协议中的重要选择。

作为Web3.0数字身份的底层支撑，secp256k1通过去中心化标识符（DID）实现了自主主权身份认证。用户通过算法生成的密钥对完全掌控自己的数字身份，无需依赖第三方认证机构，这与传统PKI体系形成鲜明对比。

在物联网领域，secp256k1为海量设备提供了轻量级认证方案。其计算效率优势特别适合资源受限的物联网终端，可实现设备间的安全通信和身份验证，为智能家居、工业物联网等场景构建可信连接。

联邦学习这一新兴的隐私计算技术也受益于secp256k1。算法在保护数据隐私的同时，允许参与方在不暴露原始数据的情况下进行协同建模。这种特性使其成为医疗、金融等敏感数据共享场景的理想选择，展现了密码学技术在隐私保护方面的创新应用。

算法的挑战与未来

secp256k1算法当前面临着量子计算时代的严峻挑战。量子计算机的Shor算法理论上可在多项式时间内破解椭圆曲线离散对数难题（ECDLP），这将直接威胁到现有加密货币的签名体系安全。美国国家标准与技术研究院（NIST）的后量子密码学标准化进程显示，格密码学（Lattice-based Cryptography）最有可能成为替代方案，其基于最坏情况下的格难题假设展现出更强的抗量子特性。

在过渡阶段，密码学界取得了两项关键突破：一是通过Schnorr签名聚合技术将secp256k1的验证效率提升40%，二是基于BLS-12-381曲线实现的可验证随机函数（VRF）为随机数生成提供了更优解。行业正在形成清晰的演进路线：短期采用混合签名方案（如ECDSA+格签名），中期部署抗量子签名算法（如SPHINCS+），长期则向全同态加密体系过渡。这种分层防御策略既保障现有系统平稳运行，又为后量子时代做好了技术储备。

结语：信任机器的数学心脏

在区块链文明的构建中，secp256k1算法如同数字世界的数学心脏，以精妙的椭圆曲线方程持续泵送着加密血液。这条看似简单的y²=x³+7曲线，实则是万亿级数字资产的守护神，用离散对数的数学难题筑起信任的铜墙铁壁。

密码学的演进永无止境，量子计算威胁与抗量子密码研发构成永恒的攻防博弈。在这场没有硝烟的战争中，secp256k1代表的密码学智慧提醒我们：真正的安全永远建立在数学之美的基础上。当私钥在曲线上舞动，当签名在区块间流转，我们见证的不仅是技术奇迹，更是人类用纯粹数学守护数字文明的坚定信念。